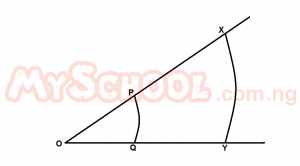
In the diagram above, PQ and XY are two concentric arc; center O, the ratio of the length of the two arc is 1:3, find the ratio of the areas of the two sectors OPQ and OXY
The correct answer is C. 1:9
Let the radius of the arc PQ = r and the radius of the arc XY = R.
Length of arc PQ = \(\frac{\theta}{360} \times 2\pi r = 1\)
Length of arc XY = \(\frac{\theta}{360} \times 2\pi R = 3\)
Ratio of the arc = \(\frac{r}{R} = \frac{360 \times 2\pi \theta}{2\pi \theta \times 360 \times 3}\)
= \(\frac{1}{3}\)
Ratio of their area = \((\frac{1}{3})^2 = \frac{1}{9}\)
= 1 : 9
Previous question Next questionWhat is Exam without Practice? With our customizable CBT practice tests, you’ll be well-prepared and ready to excel in your examsStart Practicing Now